Part-1:私钥是什么
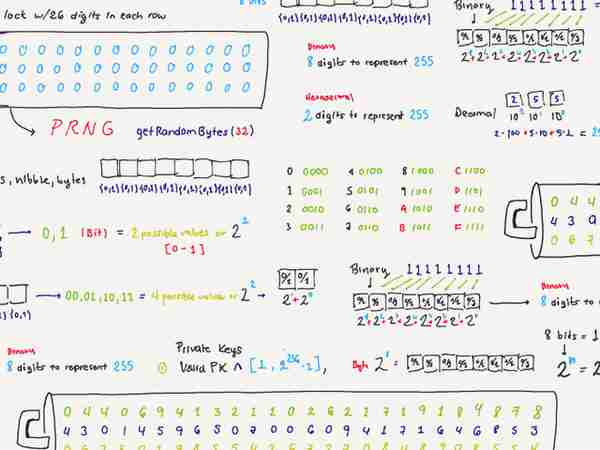
以私钥为原材料
正如我在本系列第一篇文章《私钥是什么》中所述,生成私钥的过程依赖于伪随机数生成器(PRNG)和足够大的熵。关于私钥,最重要的一点是,它是从 1 到 22??-1 的范围内随机选出的整数。只要是在这个范围内的数,都可以用作私钥。
既然我们已经初步学习了私钥背后的数学知识,接下来就可以自己生成有效的私钥了(译者注:教育目的,可跟随作者的思路学习,但不推荐自己生成。)。我们不妨将私钥生成过程想象成一个长达 78 位的水平数字组合锁(其可能组合数量恰好等于 22??-1),然后我们把这个密码锁分成 3 排,每排有 26 位。你可以把 PRNG 函数想象成一个会随机打乱数字,打乱出一个数字组合的东西:一开始每一位都是 0,然后毫无章法地在每一位上选出一个具体的数字。假设我们使用 PRNG 函数生成乱序的数字组合,得到以下三排数字:
(1) 04406941321102621719184878;
(2) 43014596507006094171646853;
(3) 06780198554267270848908554;
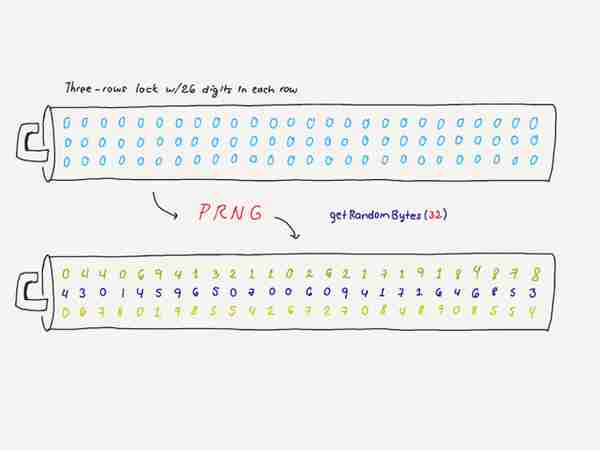
- 浏览器使用 Web Cryptography API (提供 Crypto.getRandomValues(32) 之类的密码学原语,或者等价的 32 字节缓冲区)作为 PRNG。这个 PRNG 使用你的计算机熵源 作为随机种子来生成随机数。在生成随机数的时候,请一定要使用电子熵源,因为一些研究表明,人类比较不擅长选择随机数字(人自己选出来的数字是有模式的,达不到伪随机的要求) -
恭喜!你现在已经是私钥 44069413211026217191848784301459650700609417164685306780198554267270848908554 的所有者了。
我们可以使用这个私钥生成一个比特币或以太坊地址,或者任何以 1 至 22??-1 为私钥范围的区块链的地址。
要根据这个私钥生成一个以太坊地址,我们需要使用椭圆曲线点乘算法(需要一篇专门的文章才能讲清楚)。因此,简单起见,我们会把它交给计算机处理。为此,我们需要把这个私钥“告诉”计算机。麻烦的是,计算机不会处理十进制形式的信息,它只能理解二进制代码。目前,我们的只有十进制数形式的私钥。因此,我们先要将这个私钥从十进制数形式转换为计算机可以理解的比特(bit,也译成 “位” 或 “位元”)和字节(byte,一个字节等于 8 个比特)。
位和字节
在进行下一步操作之前,我们需要先了解什么是比特和字节。任何数字设备都只能理解由 0 和 1 组成的信息,通常被称为比特。比特就是“二进制数字”,即,仅使用 1 和 0 表示的数字。虽然我们的智能手机和电脑都可以显示汉字和图片,还能播放歌曲,它们最终都是比特来表示并处理这些信息的。位越多,表示的信息越大,但说到底无非是一堆 0 和 1 而已。
根据上下文,多个位可以表示字符(如,在使用 ASCII 编码时,字母 a 的定义就是 01100001)或数字(01100001 也可以用来表示十进制数 97)。在将十进制整数转换为二进制形式时,就是将其转换成以 2 为底数的幂之和,其中每个幂的指数递增。例如,我们通常采用十进制形式记数,十进制数就是以 10 为底数的幂之和。因此,在使用二进制时,在 2 的 N 次幂以内的整数,我们就可以用 n 个位来表示和存储。
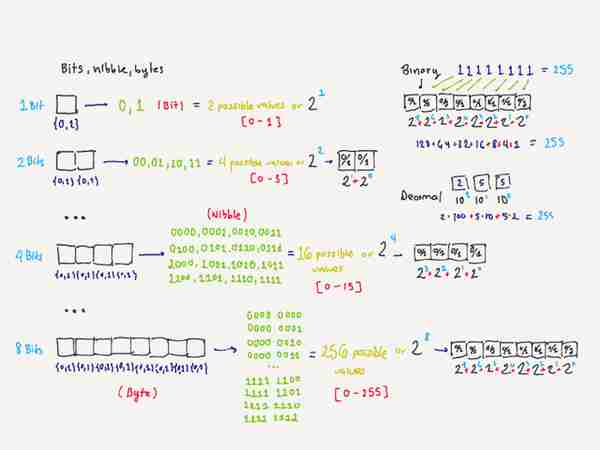
- 8 位电子游戏机最高能够表达的十进制数是 255,因为它们使用的中央处理单元(CPU)最多只能执行 8 位操作(译者注:上图的左边解释了为什么 N 个位就可以表示 2 的 N 次幂以内的数 -- 因为其数字组合有 2 的 N 次幂种可能性;右边则演示了一个二进 制数意味着多大的整数,即相互转换的计算规则 -
虽然我们可以使用二进制形式来表达任何数字,但是二进制形式过于“繁冗”。如果要表示 97,我们需要 8 个二进制数字。二进制数对于计算机来说很容易处理,但是不方便人类阅读。因此,计算机通常会使用十六进制而非二进制来表示数据:位置数字系统以 16 为底数来表示数字。一位十六进制数可表示四位二进制数。我们可以用十六进制数 61 来表示二进制数 01100001 或十进制数 97,这样就比二进制少了 6 位数。十六进制数使用 ABCDEF 来表示 10 至 15,通常用来缩小数据。
私钥有多少个比特?
再说回私钥,我们知道私钥的范围是 1 至 22??-1。我们该如何用位来表示它?需要用到多少位?如上文所述,在将十进制整数转换为二进制形式时,就是将其转换成以 2 为底数的幂之和。在使用 8 位二进制数时,我们能表示的最大的数是 2? + 2? + 2? + 2? + 23 + 22 + 21 + 2?,即,整数 255。我们可以看出,要表达 2^n 以内的数,我们就需要 n 个位。由此可推得,我们需要 256 位,或者说 32 字节(256/8),来表示我们的私钥。

- 十六进制数据表示旨在减少表示数字所需的位数。但是,计算机依然只能使用二进制来处理数据 -
如果我们一致同意需要使用 32 字节来表示我们在 [1, 22??-1] 范围内的私钥,那么在十六进制形式下,我们需要 64 个数来表示私钥。现在,我们可以将原始私钥
44069413211026217191848784301459650700609417164685306780198554267270848908554
转换成十六进制形式:
616E6769652E6A6A706572657A616775696E6167612E6574682E6C696E6B0D0A
看到十六进制私钥中多出的字母 A、B、C、D、E 了吗?看到这些字母,我们就可以轻易辨别出这个数是十六进制的。
从私钥到公钥
现在,我们可以把这个十六进制私钥告诉我们的计算机了。我们可以使用 JavaScript 之类的编程语言轻松导入这个十六进制私钥,以便用于之后的乘法运算。在以下代码中,之前得到的十六进制数被导入作为私钥(“sk”是 secret_key 的缩写,是密码学中的标准记法)。这个十六进制数是以 16 为底数的。
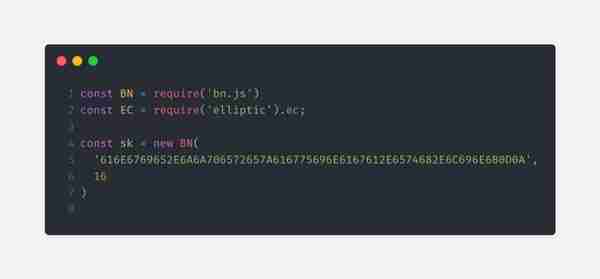
- 通过使用 BigNumber 库,我们可以确保转换过程中不会丢失任何小数。这些数字通常会被表达成指数(例如,4.406941321102622e+76),而且如果我们直接将其解析成十六进制,就会失去精度。如果不使用 BigNumber 库,我们得到的十六进制私钥就会变成 616e6769652e6c00000000000000000000000000000000000000000000000000 -
导入私钥之后,下一步就是创建公钥。你可能还记得,我们在第一篇文章中提到过,在获取以太坊地址之前,我们先要通过私钥来生成公钥。根据以太坊黄皮书所述,公钥生成过程遵循的是标准的 ECDSA 公钥生成算法,其中,我们将私钥乘以生成器点得到一个坐标,将该坐标的 x 值和 y 值前后拼在一起就是公钥。我们的公钥(在密码学中记为“pk”)可以用来生成我们的以太坊地址。
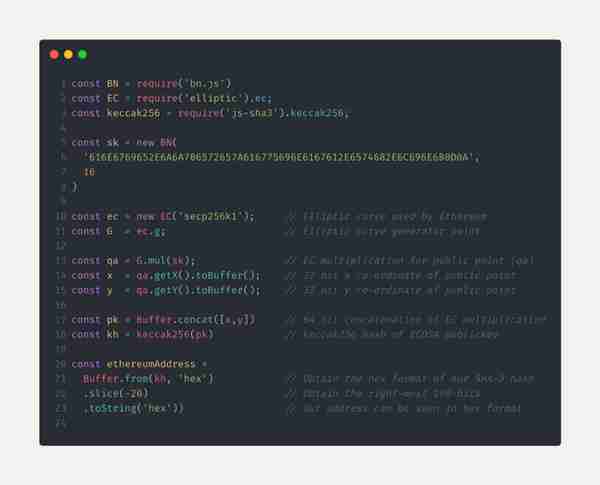
- x 和 y 是使用椭圆曲线上的点乘以我们的私钥(sk)得到的。虽然私钥可以在任意区块链中作为一个地址的唯一生成器,以 太坊专门使用椭圆曲线 secp256k1 生成公钥;因此,私钥的签名操作也跟这条曲线有关 -
终于到了最后一步。有了公钥,我们就执行黄皮书中的最后一个操作:
给定某个私钥,以太坊地址 A 是对应 ECDSA 公钥的 Keccak 哈希值的最右边 160 位。
鉴于我们已经有了自己的 ECDSA 公钥,剩下的唯一一件事是在我们的公钥上执行 Keccak 哈希函数,取结果最右边的 160 位。当我们将这些操作结果存储在“缓冲区”(就好像存储信息的小盒子)时,我们可以“丢掉”(切片)前 24 个十六进制数,只留下后 40 个十六进制数,或者更准确地说,20 个字节(这就是以太坊地址的长度)。
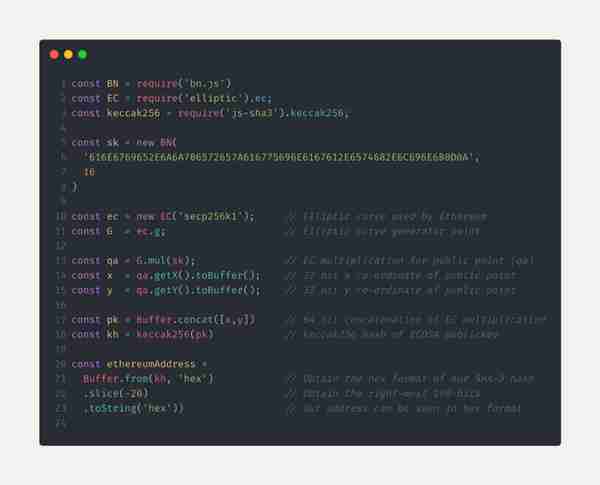
- 以太坊地址被设计为 20 个字节。有人认为删掉一些字节(具体来说是 12 个字节)可能会引起碰撞,导致两个私钥生成相同的以太坊地址。不过到目前为止,还没发生过这种情况 -
你的个人专属钱包
如你所见,只要一个数(虽然很长)就可以生成一个以太坊地址来存储各类资产:从代表虚拟猫、磁带、袜子和门票等物品的 NFT 到具有增值潜力的密码学资产等等。你的以太坊地址是公开的,而且像你的家庭住址一样,但是只能通过钥匙打开。


